一、命题逻辑
全章节思维导图
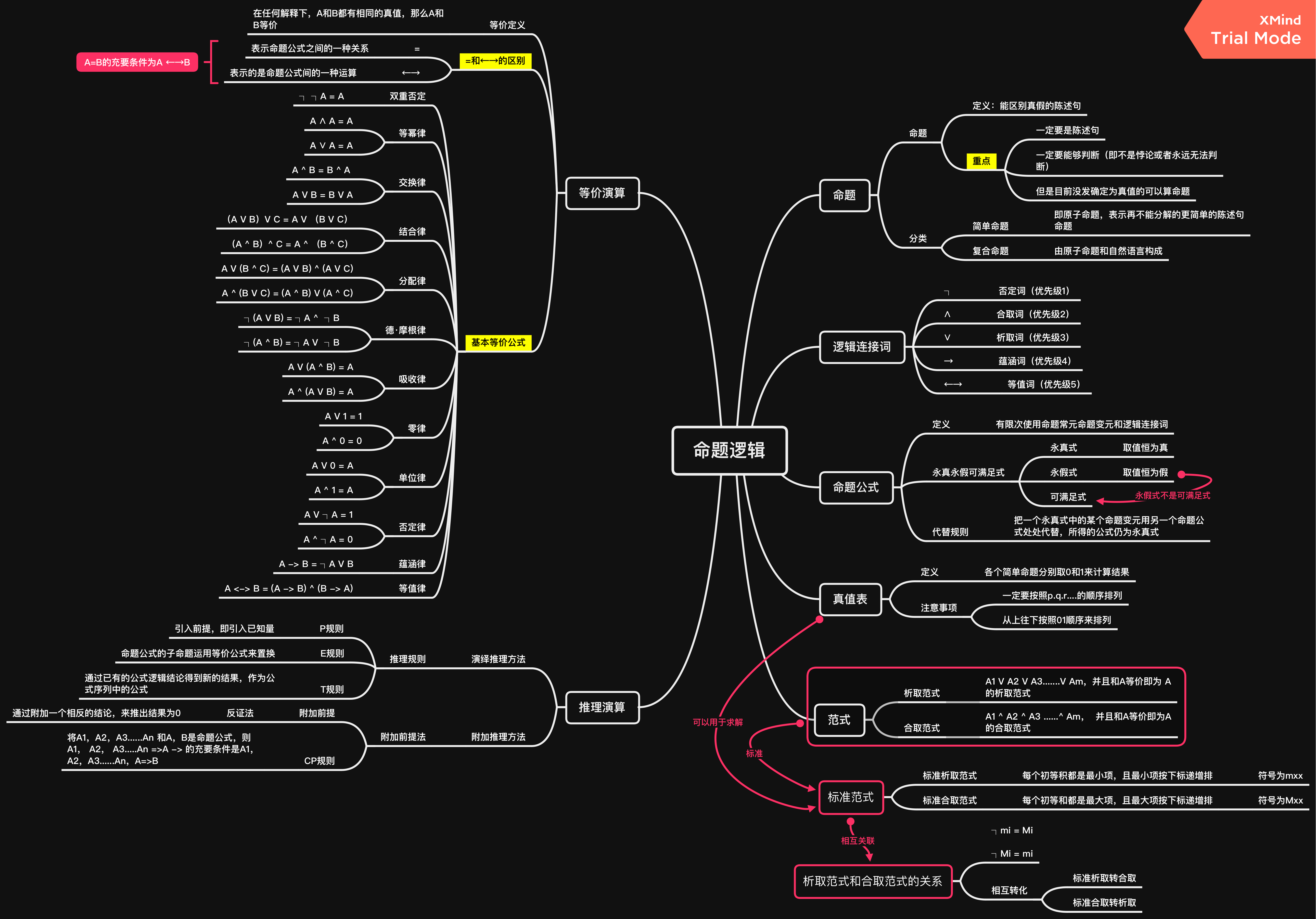
1·1 命题和逻辑连接词
注意点
连接词的优先顺序为:
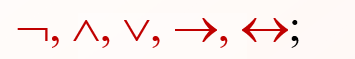
如果出现的连接词同级,又无括号时,则按从左到右
的顺序运算; 若遇有括号时,应该先进行括号中的运算.
1·3 命题公式的等价演算
基本等价式


重点为上述的5 6 11
1·4 命题公式的范式
初等和
有限个命题变元或其否定组成的析取式
初等积
有限个命题变元或其否定组成的合取式
析取范式

合取范式

1·5 命题公式的推理演算
定义
从前提开始来构造一个有限公式序列,其中每个命题公式或者是已知的前提,或者是由前面的命题公式应用推理规则得到的结论,最后使得这个公式序列中的最后一个公式即为结论。称此方法为演绎推理
定理
- P规则(前提引入规则)
在任何步骤中都可以引入前提 作为公式序列中的公式。
- T规则(结论引入规则)(可理解为整体的替换以及出答案)
在任何步骤中都可以将已有公式的逻辑结论作为序列中的新公式。
- E规则(置换规则)(可理解为用公式进行计算)
在任何步骤中都可以用公式中的命题公式等价的公式作为序列中的新公式。
- 附加前提法1(CP规则)
将非B加入前提,若推出矛盾(0),则得证推理正确.
二、谓词逻辑
全章节思维导图
2·1 个体词、谓词与量词
全称量词
存在量词
2·3 谓词公式的等价演算
基本等价式第一组(同1.3 的基本等价式)
基本等价式第二组
量词否定律
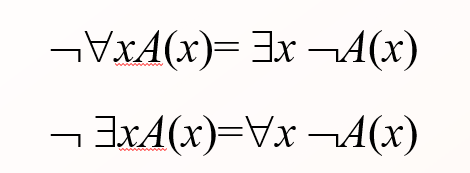
量词辖域收缩与扩张律

量词分配律

量词交换律
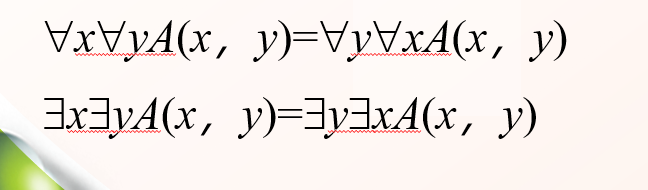
前束范式

2·4 谓词公式的推理演算
推理规则
US规则(全称量词消去规则)

ES规则(存在量词消去规则)

注意事项
所有4个量词的推理规则都只能在前束范式中使用。
先ES后US 先是存在量词的引入,再是全称量词的引入
三、集合与关系
全章节思维导图
3·1 集合及运算
幂集

计数
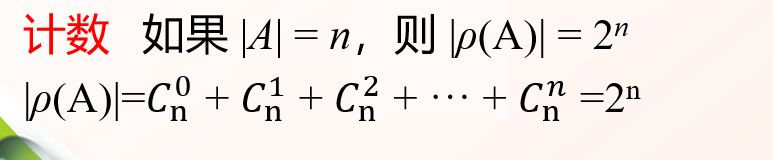
集合的基本运算

需要注意的是这里的第五个即对称差!
集合的运算性质

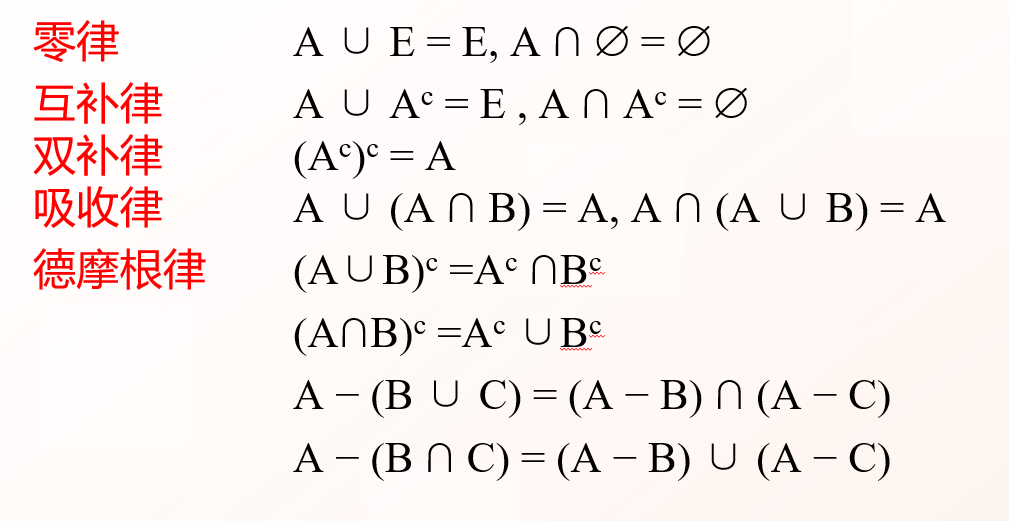
重点为第二张图
3·2 二元关系及其运算
序偶定义
由两个元素 x 和 y,按照一定的顺序组成的二元组称为有序对,记作<*x*,*y*>,通常称为序偶。
序偶性质
有序性
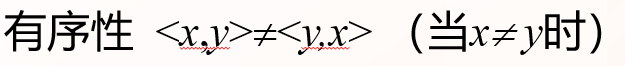
元组定义

笛卡尔积

笛卡尔积的性质

二元关系

复合关系
简单理解为传递关系
3·3 二元关系的性质与闭包
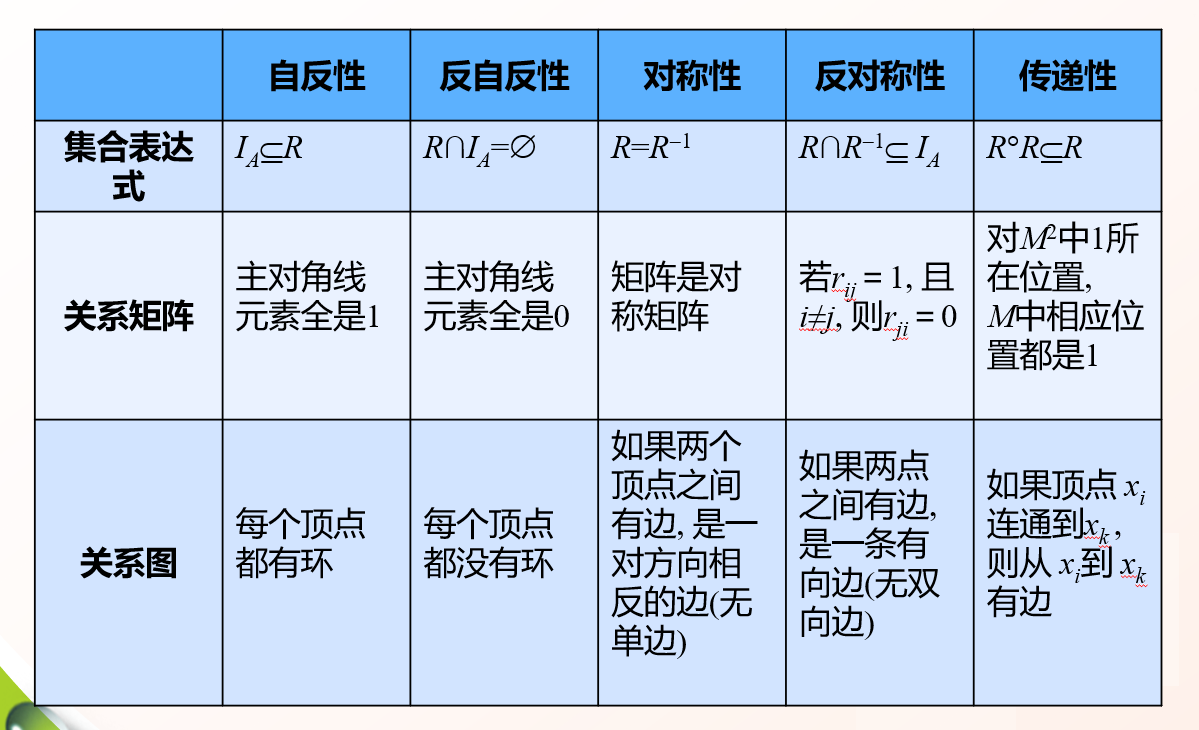
关系的5个性质
自反性
对角线全为1
反自反性
对角线全为0
对称性
关于对角线对称
反对称性
所有的点与对角线非对称
传递性

有序性图的基本概念
5·1 图的基本概念
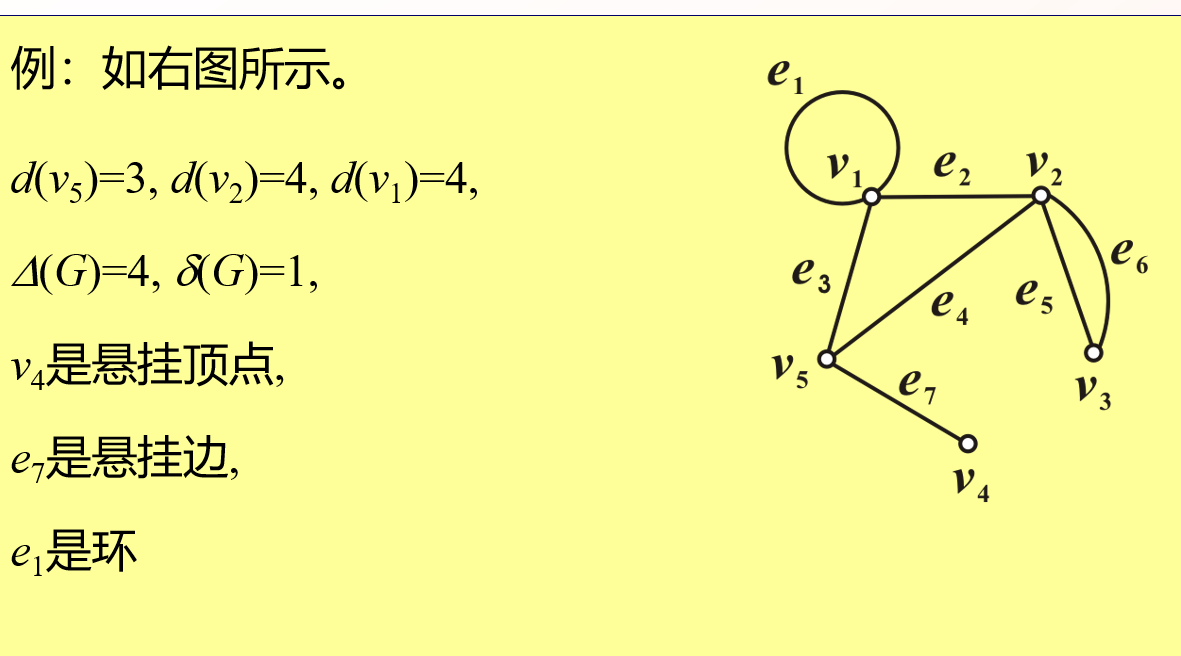
平凡图表示G(1,0)及图中只有一个孤立点,否则不是
|R(V1 )|表示图G中连接点集V1 外部与内部点的边的条数
设G是(p, q)简单图,若δ(G) = D(G) = r ,则称G是r度正则图。
p − 1度正则图称为完全图,记为Kp
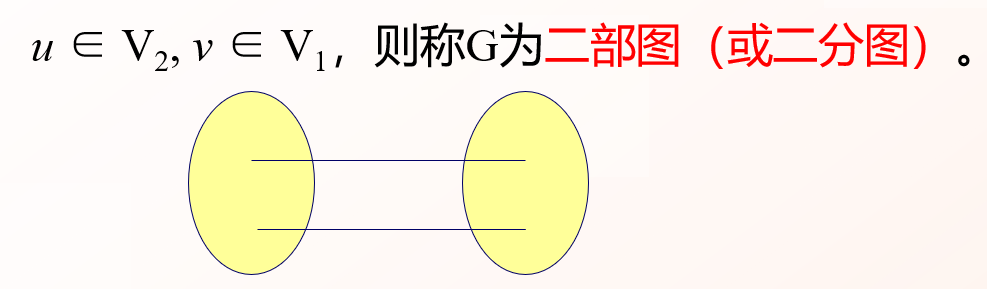
设G = ⟨V, E⟩是简单图且V=V1∪V2, V1∩V2=∅。若∀(u,v) ∈ E,均有u ∈ V1, v ∈ V2或u ∈ V2, v ∈ V1,则称G为二部图(或二分图)
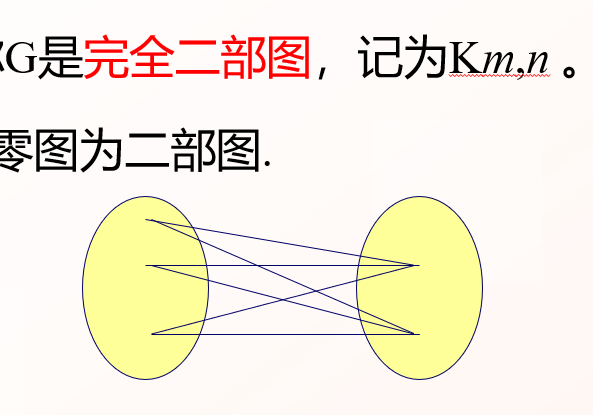
是否可图化
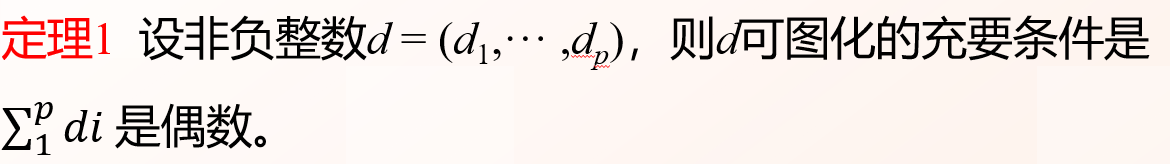

补图

5·2 图的连通性
定义

简而言之
能从头走到尾即位通路其中,如果这条通路首尾相连,那么又称为回路。
如果上面的路中没有重合边则为简单通路/回路。
如果上面路中没有经过一个点两次及以上则成为基本通路/回路。(路径/圈)
基本回路判定
如果非零图G中无奇点,则G中必有基本回路。
图中的距离

连通分图
非连通图G中的极大连通子图。也就是V关于连通关系R的等价类的导出子图。
连通图的判定定理
1:若一个图中恰有2个奇点,则这2个奇点之间连通。
2:在p阶简单图G中,若对G的每对顶点u,v,都有
d(u) + d(v) ≥ p − 1, ∀u, v ∈ V
则G是连通图。
证明:用反证法。若G不是连通图,则它至少有二个连通分
图,设其中一个连通分图有n个(n ≥)顶点,u**0是其中的一个顶
点,其余各连通分图共含有p-n个顶点, v**0是其中的一个顶
点.则d(u**0) ≤ n − 1, d(v**0) ≤ p-n − 1
二式相加得d(u**0) + d(v**0) ≤p− 2
推论 在p阶简单图G中,若 δ(G) ≥ (p−1)/2,则G是连通图。
3: (p, q)简单图G若有k个连通分图,则边数
q ≤ (p−k)(p−k+1) /2
4:若(p, q)图G是连通图,则q ≥ p − 1 。
证明:用数学归纳法。
p=1时, q=0
假设p ≤n时,有q ≥ p − 1
当p= n +1时,可以看作n个顶点的图加一个顶点,因为是连通图,这个顶点与n个顶点的图至少有一条边相连,因此
q ≥ n − 1+1,即q ≥ (n+1 )− 1= p − 1
5:简单图G=<V*,E>是二部图当且仅当G*中没有长度为奇数的基本回路。
图的删除
G-v: 从G中删除v及关联的边
G-V ¢: 从G中删除V ¢中所有的顶点及关联的边
G-e : 从G中删除e
G-E¢: 从G中删除E¢中所有边
点割集
设图G=<*V*,*E*>, 点子集V1 ⊆ V , 若
(1)G- V1是平凡图或其连通分图数大于G的连通分图数
(2)∀V2⊂ V1, G- V2的连通分图数不大于G的连通分图数
则称V1为G的点割集.
若V1={v}为点割集, 则称v为割点.
边割集:
设图G=<*V*,*E*>, 边子集E1 ⊆ E , 若
(1)G- E1是平凡图或其连通分图数大于G的连通分图数
(2)∀E2⊂ E1, G- E2的连通分图数不大于G的连通分图数
则称E1为G的边割集. 简称割集。
若E1={e}为割集, 则称e为割边或桥.
点连通度
图G = ⟨V, E⟩的点连通度是指为了由G产生一个不连通图或者平凡图,而需从G中去掉的最少的顶点数,记为κ(G)
κ(G)=min{|V1| V1为G的点割集}
- 性质1 非连通图和平凡图的点连通度是0
- 性质2 连通图中若有割点,则点连通度是1。
- 性质3 κ(Kp)=p − 1
边连通度
图G = ⟨V, E⟩的边连通度是指为了由G产生一个不连通图或者平凡图,而需从G中去掉的最少的边数,记为λ(G)
λ(G) =min{|E1| E1为G的割集}
- 性质1 非连通图和平凡图的点连通度是0
- 性质2 连通图中若有割点,则点连通度是1。
- 性质3 λ(Kp)=p − 1
5.4 图的矩阵表示
G的邻接矩阵
设G=<V*,E>是p阶图, 其中V*={v1, v2, …, vp}, p阶方阵 AG=( aij )p´p为图G的邻接矩阵, 其中元素aij为起点vi终点vj的边的数目。
简单表示即 竖着表示V1 V2 V3 V4…的点 横着表示V1 V2 V3 V4…的点,数字表示有几条线
0表示不连接
n表示有n条线
成环时即主对角线上相应的点值为1(不是2)
G的关联矩阵
设G=<V*,E>是(p,q)图, V={v1, v2, …, v**p}, E={e1, e2, …, e**q}, p×q阶矩阵 MG=( m**ij )p´q为图G的关联矩阵, 其中元素mij为vi与e**j的关联次数。

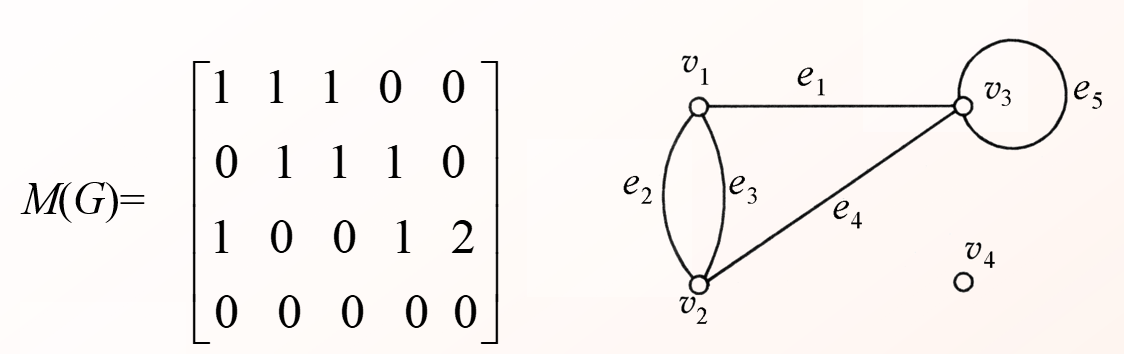
简单表示即 竖着表示V1 V2 V3 V4…的点 横着表示e1 e2 e3 e4…的线
1表示有关联;
0表示无关联;
2表示成环
例题:
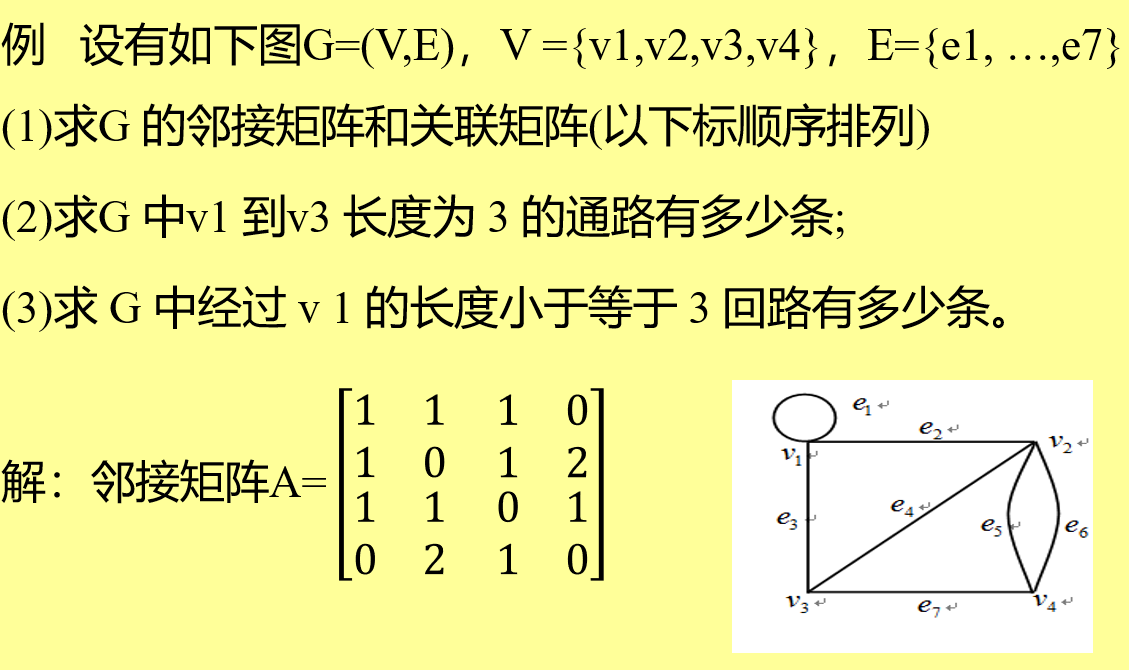
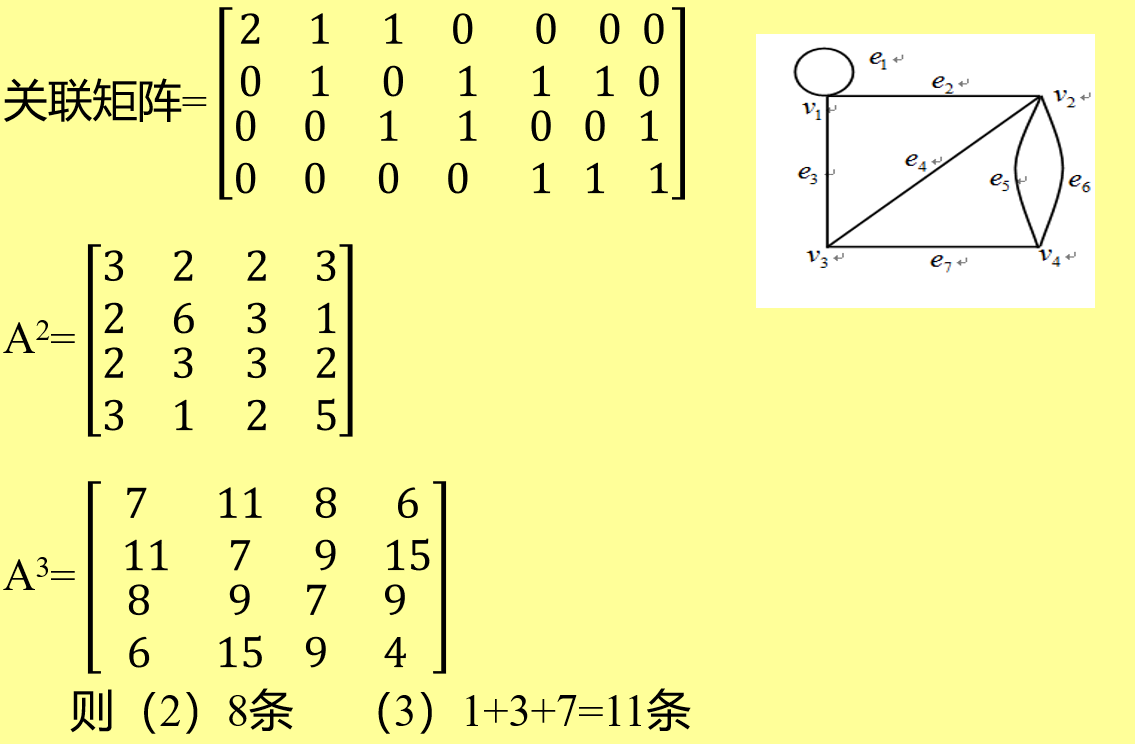
带权图

其中的L1 L2…都是题目提供的
5.5 树
树
- 无基本回路的连通图
平凡树
- 平凡图
森林
- 每个连通分图都是树的非连通图
树叶
- 树中度数为1的顶点
分支点
- 树中度数大于等于2的顶点
等价关系
- G中任意两个顶点之间存在唯一的基本通路
- G是连通的且G中任何边均为桥
- G是连通的且q=p-1
- G中无回路且q=p-1
- G中没有基本回路, 但在任何两个不同的顶点之间加一条新边后所得图中有唯一的一个含新边的基本回路。
阶数的计算
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
定理
- 设T是连通图G的一棵生成树, 则
- G的任何基本回路都至少包含T的一条弦
- 若e为T的弦,则G中存在一条且只存在一条只含弦e**,其余都是枝的基本回路,称为G的对应T的弦e的基本回路
- G的任一割集都至少含有T的一条枝
- 若e为T的枝,则G中恰好存在一个只含枝e**,其余都是弦的割集,称为G的对应T的枝e的基本割集。
求基本回路的算法
设弦e=(u,v), 先求生成树T中u到v的基本路
径G**uv, 再加上弦e.
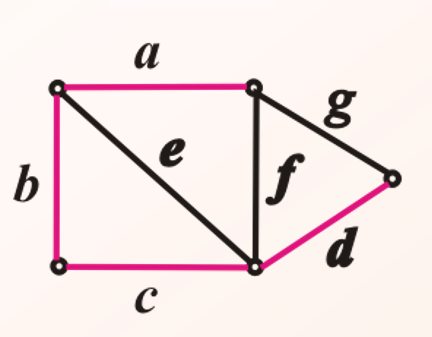
例如上图红色的是枝,黑色的是弦
Ce=(e,b, c), Cf=(f, a, b, c),
Cg=(g, a, b, c, d)
(即只能过一条弦)
求基本割集的算法
设a为生成树T的树枝, T-a由两
棵子树T1与T2组成, 则
Sa={e | eÎE(G)且e的两个端点分别属于T1与T2} .

例如上图红色的是枝,黑色的是弦
则Sa={a, f, g}, Sb={b, e, f, g},
Sc={c, e, f g}, Sd={d, g}
(即只能割一条枝)
回路合并
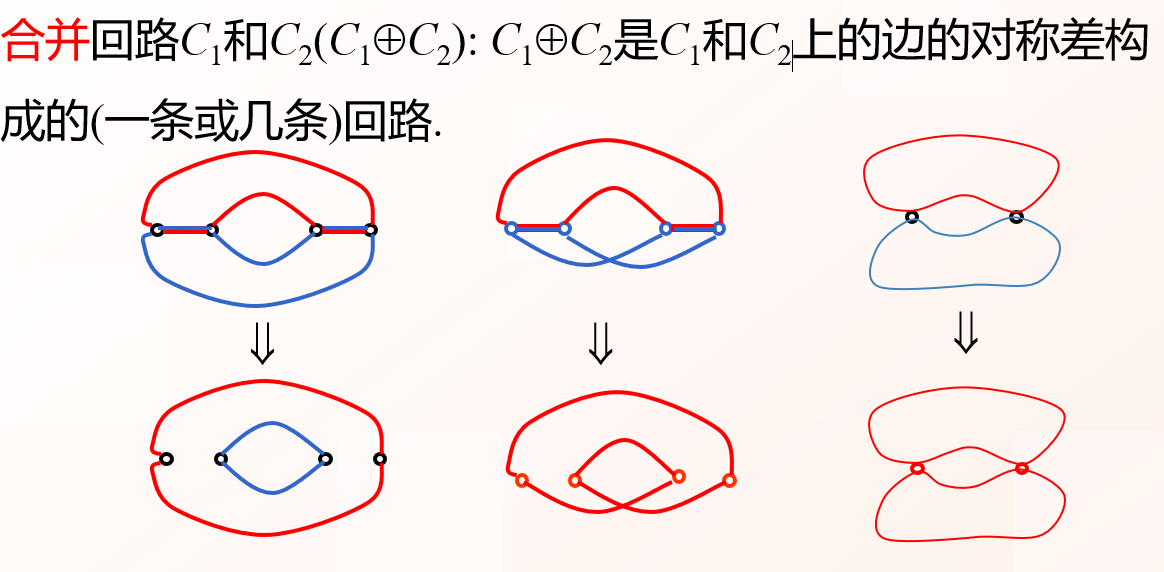
基本回路的性质
连通图中的任一条回路都可以表成对应它所含弦的基本回路
的合并.

例如, abcf=Cf
aef=Ce困Cf
aedg=Ce困Cg
bcdgfe=Ce困Cf困Cg
基本割集的性质
连通图中的任一割集都可以表成对应它所含树枝的基本割集
的对称差.

例如 {g,d}=S**d
{a,b,e}=S**aÅS**b
{a,e,c}=S**aÅS**c
{b,e,f,d}=S**bÅS**d
5.6 最小生成树
最小生成树
- 带权图中权最小的生成树
Kruskal算法基本描述
(1)先构造一个只含 n 个顶点,而边集为空的子图,若将
该子图中各个顶点看成是各棵树上的根结点,则它是一个含
有 n 棵树的一个森林。
(2)从带权图的边集 E 中选取一条权值最小的边,若该条
边的两个顶点分属不同的树,则将其加入子图,也就是说,
将这两个顶点分别所在的两棵树合成一棵树;反之,若该条
边的两个顶点已落在同一棵树上,则不可取,而应该取下一
条权值最小的边再试之。
(3)依次类推,直至森林中只有一棵树,也即子图中含有 n-1条边为止。
Prim算法基本描述
(1)初始化:Vnew= {v},其中v为集合V中的任一节点(起始点),Enew= { }(空集)。
(2)重复下列操作,直到Vnew= V:
①在集合E中选取权值最小的边<u, v*>,其中u*为集合Vnew中
的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一)。
②将v加入集合Vnew中,将<*u, v*>边加入集合Enew中;
(3)使用集合Vnew和Enew来描述所得到的最小生成树。
5·7 欧拉图与哈密尔顿图
欧拉图
欧拉通路:
图中行遍所有顶点且恰好经过每条边一次的通路.
欧拉回路:
图中行遍所有顶点且恰好经过每条边一次的回路.
欧拉图:
有欧拉回路的图.
半欧拉图:
有欧拉通路,但无欧拉回路的图.
额外说明
规定平凡图为欧拉图.
欧拉通路是简单通路, 欧拉回路是简单回路.
环不影响图的欧拉性.
欧拉图定理
- 图G是非平凡的连通图,则G是欧拉图当且仅当G中无奇点。
证明1
若G是连通的而且是欧拉图,则欧拉回路既包含所有的边,也包含所有顶点。对该欧拉回路上的每一个顶点,若有一条边以该顶点为出发点,必然对应另一条边以该点为终止点。因为这样的边成对出现,并且不重复,所以每个顶点的度数必然为偶数。
- 图G是非平凡的连通图,则G是半欧拉图当且仅当G恰有两个奇点,而且这二个奇点即是欧拉通路的起点和终点。证明:
证明2
若G是连通的而且是半欧拉图,则欧拉通路包含所有的边,也包含了所有顶点。沿着该欧拉通路前进,则只有起点和终点经过奇数次,其他顶点必然经历偶数次,即入顶点和出顶点的次数成对,所以G中恰有两个奇点。
- 若连通图G中恰有2n个奇点,则G可以表示为至少n条简单通路的边不相交的并。
哈密尔顿图
哈密顿通路:
经过图中所有顶点一次且仅一次的通路.
哈密顿回路:
经过图中所有顶点一次且仅一次的回路.
哈密顿图:
具有哈密顿回路的图.
半哈密顿图:
具有哈密顿通路而无哈密顿回路的图.
几点说明
平凡图是哈密顿图.
哈密顿通路是基本通路,哈密顿回路是基本回路.
环与平行边不影响图的哈密顿性.
注意点
每个哈密尔顿图都连通
哈密尔顿图的每个顶点的度数大于等于2
一个图若有哈密尔顿回路,则 度数为2的顶点所关联的两条边一定在哈密尔顿回路上。
若某图有哈密尔顿回路,则 必须在该哈密尔顿回路中出 现的边不能构成一个未经过 所有顶点的回路
定理
若G是(p, q)简单图,且p ≥ 3,若对于G中任意二点u, v都有
d(u) + d(v) ≥ p
则G是哈密尔顿图。
若G是(p, q)简单图,且p ≥ 2,若对于G中任意二点u, v都有
d(u) + d(v) ≥ p*-*1
则G是半哈密尔顿图。
设G是哈密尔顿图,从G中任意去除k个点以及与之关
联的边后所得到的图记为G’,则G’的连通分图数不超过k。
也即对于任意V1ÌV且V1¹Æ, 均有 p(G-V1)£|V1|.
证:设C为G中一条哈密顿回路, 有p(C-V1) £ |V1|. 又因为
CÍG, 故 p(G-V1) £ p(C-V1) £ |V1|.


